Seconda puntata (qui la precedente) dell’analisi sui numeri di Tesla Model S Plaid realizzata da Massimo Ceraolo, Professore di Veicoli Elettrici e Ibridi presso Ingegneria dei Veicoli all’Università di Pisa. Ceraolo ha usato un simulatore per verificare le prestazioni e il comportamento della super performante vettura presentata da Elon Musk. Ecco cosa ha scoperto
di Massimo Ceraolo
Nella tecnica ingegneristica si usa moltissimo simulare gli oggetti di cui abbiamo generato un modello matematico. Nella simulazione, in sostanza, seguiamo nel tempo quello che succede nella nostra auto, senza averla a disposizione, analizzandone quello che il suo modello fa. Se il modello è sufficientemente accurato, i risultati che otterremo dalla simulazione saranno sufficientemente prossimi a quello dell’oggetto reale.
Questo è fondamentale nella fase di progettazione, in quanto l’oggetto non è ancora costruito e la simulazione ci consente di prevederne il comportamento futuro. Per noi, invece, la simulazione è uno strumento di valutazione virtuale delle prestazioni della Tesla Model S Plaid, in quanto non ne abbiamo a disposizione un esemplare (e anche se l’avessimo potrebbe essere complicato e costoso fare tutti i test).
In questo articolo vi presento il simulatore e i risultati del simulatore così come lo uso nel mio PC. Mi piacerebbe molto, ma non so se ci riuscirò, realizzare un simulatore on-line, talmente semplice da utilizzare che chiunque, collegandosi mediante il sito di VaiElettrico, potesse fare le prove che vuole. Ad esempio cambiando il raggio della ruota, il Cx, la massa del veicolo ecc., per vedere l’effetto che fa. Ripeto, non so se ci riuscirò. Per ora accontentiamoci di seguire nell’articolo delle semplici simulazioni fatte off-line.
Cosa c’è e come funziona un simulatore
Il simulatore che userò è basato sul linguaggio Modelica e sulla libreria Modelica Standard Library. Questo linguaggio e questa libreria consentono di realizzare graficamente modelli, che hanno una struttura estremamente simile a come la rappresentiamo nei nostri schemi sui libri.
Vediamo quindi, nella seguente figura 1, che aspetto ha il modello che useremo, e confrontiamolo con lo schema già visto nell’articolo articolo “I numeri di Tesla Model S Plaid: meglio di una F1” che riportiamo a seguire per comodità.
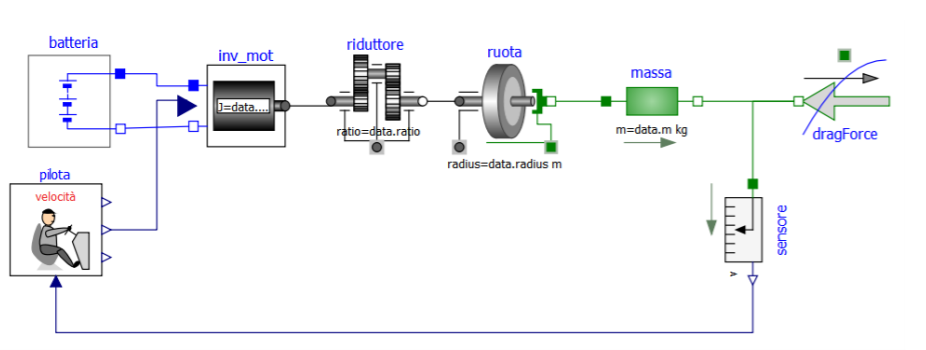
Dovrebbe essere facile riconoscere nel modello gli elementi presenti nella figura: la batteria, l’inverter e il motore (qui uniti a formare un unico componente, come spesso accade anche fisicamente nelle auto), il riduttore, la ruota.
Il modello è completato dalla forza “dragForce”, che è la resistenza al moto di cui abbiamo tanto parlato nell’articolo. Contiene inoltre il pilota, che attraverso il suo pedale di accelerazione (il filo blu che esce dalla sua icona) richiede al gruppo inverter-motore una certa coppia.
In questo modello, per semplicità, immaginiamo di avere una guida one-pedal, come è ad esempio quella della Nissan Leaf, che consente con il solo pedale dell’acceleratore sia di accelerare che di frenare (salvo frenate di emergenza). Per accelerare la coppia richiesta sarà un valore positivo, per frenare un valore negativo.
Possiamo immaginare che il pilota controlli il veicolo per far sì che la velocità nel tempo sia prossima a quella che lui desidera. Questo corrisponde anche alle modalità con cui si provano i veicoli. Sappiamo tutti che fino al 2017 i veicoli nell’Unione Europea venivano provati con il ciclo NEDC, e ora vengono provati con il WLTC (spesso si menziona WLTP). Quindi il pilota potrebbe avere in mente uno di questi cicli da riprodurre, ed esercita il comando del veicolo, nel nostro caso attraverso il pedale unico, per far sì che la
velocità sia prossima a quella prevista dal ciclo.
Ma cosa c’è dentro le varie scatolette che compongono il modello? Ovviamente non ci sono oggetti fisici, ma solo formule matematiche e poco più. Ovviamente per ognuno
degli oggetti si possono usare modellazioni semplici o complicate e di conseguenza sarà più o meno semplice o complicato quello che metteremo all’interno di ognuno degli oggetti. Per questo articolo scegliamo modelli molto semplici, ma che sono comunque in grado di darci risultati numerici realistici.
Ecco cosa c’è nella nostra implementazione dei vari blocchetti:
• Il pilota. Il nostro modello di pilota è semplicissimo: legge dal “sensore” la velocità effettiva del veicolo, ed ha in mente la velocità che vuole avere istante per istante (la scritta rossa “velocità” sopra la sua testa). Di conseguenza agisce aumentando la pressione sul pedale di acceleratore, per richiedere una maggiore coppia se la velocità è inferiore a quella desiderata, riducendola se è superiore.
• La batteria. Qui abbiamo un modello semplicissimo, che è composto da una tensione in serie con una resistenza interna. Non entro nel merito di cosa questo voglia dire; comunque, la scelta del modello della batteria non ha alcuna influenza sui risultati che vogliamo ottenere in questo articolo, quindi non vale la pena discuterla oltre.
• Il gruppo inv_mot. Questo rappresenta l’insieme di inverter e motore. Esso ha il compito di trasferire al suo albero di uscita, a sua volta collegato al primario del riduttore la coppia che il pilota sta richiedendo. Però deve contenere la curva di limitazione della potenza della Tesla Plaid. Sì, proprio la curva fornita da Musk nella conferenza di presentazione dell’auto, dalla quale siamo partiti nell’articolo precedente
• Riduttore. Il suo compito è semplicissimo ed è stato descritto matematicamente nell’articolo Veicoli elettrici-5
• Ruota. Svolge il ruolo delle ruote motrici. Essa trasforma le grandezze da “rotazionali” (quelle di un albero che ruota e che trasmette la potenza come prodotto di coppia e velocità angolare) in “traslazionali” (quelle di un oggetto che trasla, la nostra auto, e che trasmette la potenza come prodotto di forza e velocità)
• Massa. E’ la massa del nostro auto posta pari, come si è visto in Veicoli-elettrici-5, a 2322 kg. Si collega al resto del veicolo mediante due quadratini. Il quadratino verde pieno, a sinistra, contiene la forza di scambio fra le ruote motrici e la strada; quello vuoto a destra, la forza che si oppone al moto per via degli attriti e della resistenza dell’aria. Queste due forze sono uguali fra di loro solo (nella marcia in piano) quando il veicolo viaggia a velocità costante; durante le accelerate la forza del quadratino pieno supera quella di quello bianco, durante le frenate è il contrario.
• dragForce. Contiene la descrizione della resistenza al moto, esattamente come l’abbiamo analizzata nel paragrafo “la resistenza al moto della plaid” dell’articolo “I numeri di Tesla Model S Plaid: meglio di una F1“..
Con questo semplice modello possiamo analizzare il comportamento della nostra auto in varie condizioni di funzionamento.
Tesla Plaid, partenza con il piede “leggerero”
Un esempio che consente di capire come funziona la nostra auto, ma più in generale tutte le auto elettriche, può essere costituito da una semplicissima richiesta di velocità: accelerazione, velocità costante, frenata. Qui non vogliamo ancora sfruttare l’enorme coppia e potenza della Plaid; per questo scegliamo accelerazioni e velocità abbastanza tranquille.
Naturalmente per fare questa simulazione dovremmo sapere quanta potenza riesce a recuperare la Tesla Plaid in frenata, in funzione della velocità. In altre parole, dovremmo avere un diagramma analogo a quello della figura, ma relativo alle frenate a recupero, non alla trazione. Relativo cioè a flussi di potenza dalla strada verso la batteria, non viceversa.
Purtroppo questo diagramma non ce l’abbiamo e quindi dobbiamo inventarcelo. L’ipotesi che faccio qui è che il diagramma della potenza per le frenate a recupero abbia esattamente lo stesso andamento di quello in trazione. Nella realtà non è normalmente così. Normalmente le auto hanno delle potenze per le frenate a recupero inferiori a quelle erogabili in trazione. Ci sono però eccezioni illustri.
Ad esempio i diagrammi dei motori della Toyota Prius seconda serie, pubblicati in un articolo scientifico da ingegneri della Toyota, mostra una perfetta simmetria fra le potenze (e quindi le coppie) erogabili in trazione e quelle assorbibili nelle frenate a recupero.
Immaginiamo inoltre di avere un pilota estremamente reattivo. In grado quindi, con abile movimento del piede sul pedale dell’acceleratore one-pedal, di far sì che il veicolo segua accuratamente il profilo di velocità desiderato.
Nella seguente figura possiamo vedere l’andamento della velocità come abbiamo pensato di realizzarlo, quindi, come si diceva, accelerata, velocità costante, frenata. Ovviamente l’accelerazione è costante e positiva durante la rampa di crescita della velocità, costante e negativa durante la decrescita.
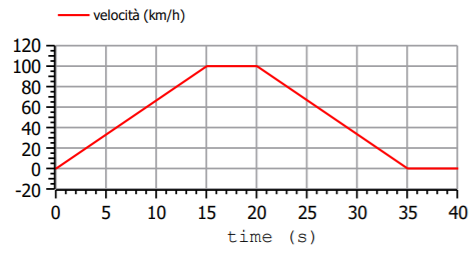
Con un pilota molto reattivo, come nel nostro caso, la velocità effettiva coincide con quella desiderata, e quindi l’andamento mostrato nella precedente figura è relativo ad entrambe.
Gli andamenti della forza di scambio fra le gomme e l’asfalto (in realtà la somma delle forze di scambio fra tutte le ruote e l’asfalto) e della resistenza al moto sono i seguenti:
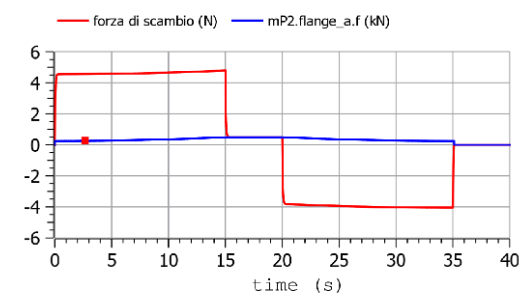Si vede che la forza per vincere la resistenza al moto (curva blu) , è una parte molto piccola della forza messa in campo dalle ruote (curva rossa). La differenza fra le due curve è il prodotto della massa del veicolo per l’accelerazione. In sostanza serve per accelerare il veicolo nel tratto iniziale a velocità crescente, e decelerarlo nel tratto finale a velocità decrescente. Proprio perché la differenza è proporzionale all’accelerazione, essa è zero nel tratto a velocità costante, in quanto in quel tratto l’accelerazione vale zero.
Ricordiamoci che 4000N di forza sono circa 400 kg. Niente male per un’accelerazione che per noi è molto tranquilla!
Guardiamo ora, nella prossima figura, le potenze.
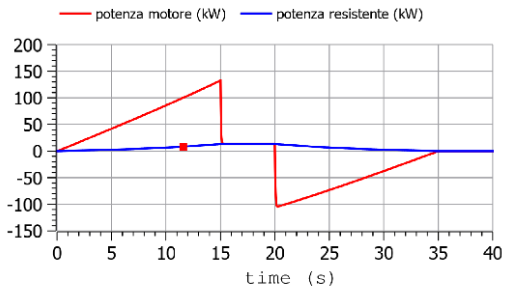
Come si vede la potenza per vincere la resistenza al moto (blu) è molto piccola rispetto a quella erogata dal motore. Dove và l’eccesso di potenza? In accumulo in energia cinetica del veicolo. In sostanza l’area compresa fra la curva rossa e la blu è l’energia cinetica accumulata durante l’accelerata e disponibile per il recupero durante la frenata successiva.
Se il motore e l’inverter avessero efficienza del 100% ovviamente impossibile (ma oggi ognuno dei due può raggiungere anche 95%) durante la frenata tutta l’energia cinetica verrebbe inviata nuovamente in batteria. E l’unica energia dissipata per sempre sarebbe la piccola area sotto la cuva blu.
Se invece di un veicolo elettrico abbiamo un veicolo tradizionale, l’area in accelerata fra la curva rossa e la blu va sempre in energia cinetica, la quale però viene poi tutta “buttata via”, cioè dissipata nei freni durante la successiva frenata.
La potenza ha il tipico andamento triangolare. Parte ovviamente da 0 perché a velocità nulla la potenza sempre nulla (è quindi profondamente errato quello che molti dicono che nei veicoli elettrici la potenza è tutta immediatamente disponibile alla partenza. Casomai si può dire della coppia che è immediatamente disponibile alla partenza).
La ragguardevole massa della nostra auto fa sì che per un’accelerata molto tranquilla 0-100 occorre, se si usa durante l’accelerata coppia praticamente costante come nel nostro caso, una potenza di picco non da disprezzare, pari a circa 132 kW.
Per confronto guardiamo nelle prossime figure coppia e potenza nel caso in cui l’accelerata e la frenata durino la metà del caso precedente:
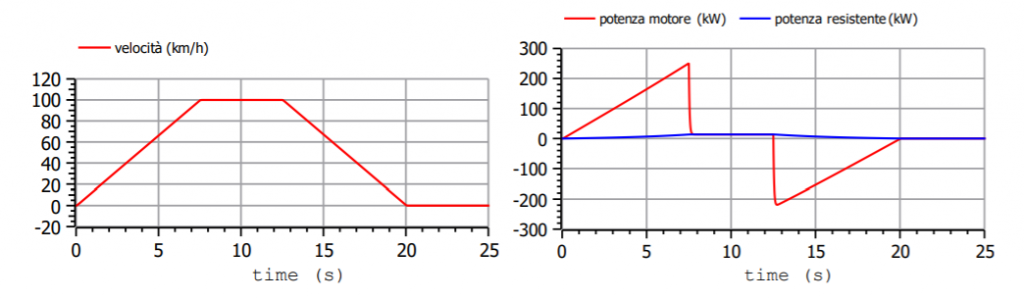
Ovviamente la potenza per vincere la resitenza al moto è rimasta invariata (curva blu), ma la potenza necessaria per fare l’accelerata ha ora un picco di 250 kW.
Accelerazione pura: la Tesla Plaid “a tavoletta”
Proviamo ora a fare un’accelerata a “tavoletta”. Così potremo vedere quanto ci mette la macchina del nostro modello ad arrivare a100 km/h, o anche a 60 miglia l’ora, quanto ci mette per i 400 metri da fermo (e il quarto di miglio), e quale è la velocità di uscita nei vari casi.
Ecco cosa succede della velocità se nella Tesla Plaid, stanti i dati che abbiamo recuperato e che sembrano particolarmente credibili, si fa un’accelerata con il piede a tavoletta per 16 secondi (inutile andare oltre in quanto a 16 secondi si raggiunge la massima velocità dell’auto, che è 200 miglia all’ora):
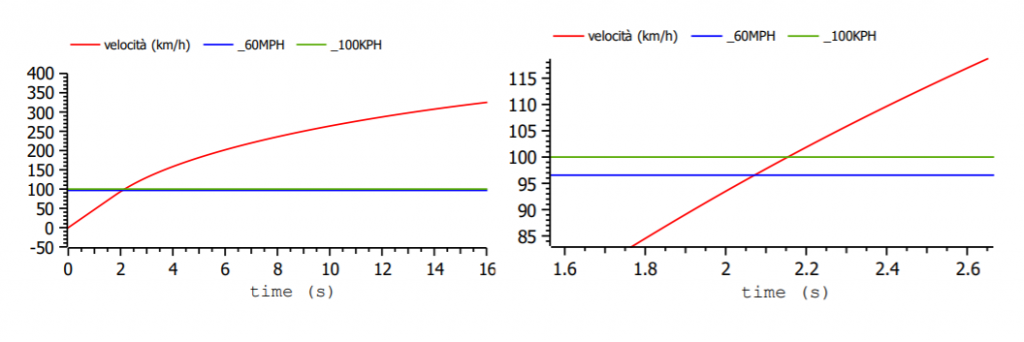
Vediamo che la velocità di 60 miglia all’ora, di poco inferiore ai 100 km/h, nel nostro modello è raggiunta dopo 2,07s. Non sono proprio i 1,99s che ha dichiarato Musk ma ci possiamo accontentare. Evidentemente i dati di cui disponiamo, pur buoni, non sono del tutto accurati.
Guardiamo ora gli spazi percorsi.
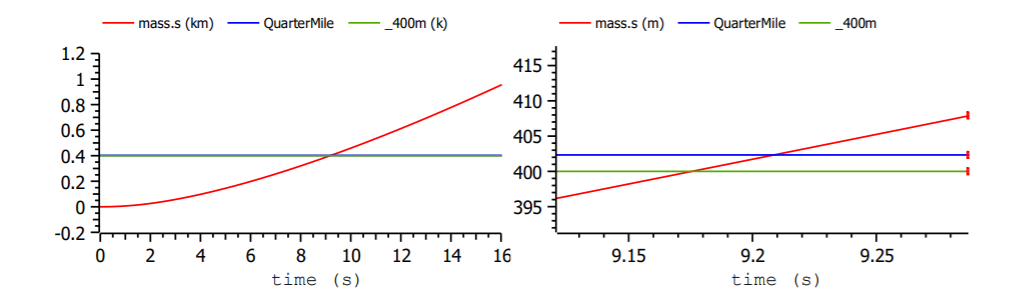
Qui osserviamo che il quarto di miglio (riga “QuarterMile) è raggiunto in 9,21s, valore molto prossimo a quello ricavabile da insideevs plaid, pari a 9,3s.
Infine, l’andamento della potenza erogata dal motore, posta a confronto con la potenza che serve a vincere la resistenza al moto:
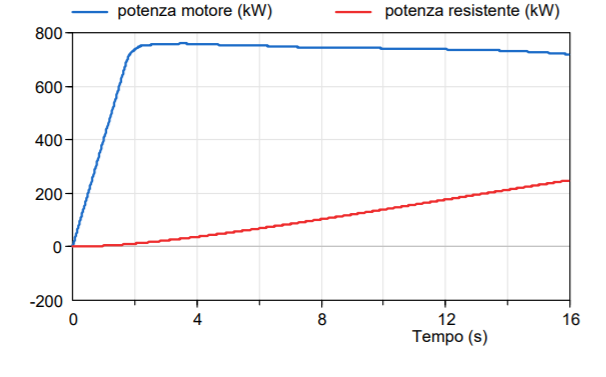
Si vede come gran parte della potenza erogata serve anche in questo caso per vincere la resistenza al moto, anche se, vista la grande velocità raggiunta nella seconda parte della simulazione della nostra Tesla Plaid virtuale, quella che serve per vincere la resistenza al moto è comunque ragguardevole e supera i 200 kW nella parte finale.
La potenza di picco prodotta dal motore (l’equivalente dei tre motori fisicamente presenti nell’auto) è 760 kW, come da dati di Musk, che corrispondono a 1020 HP.
Infine analizziamo nella seguente figura la forza di trazione e quella resistente.
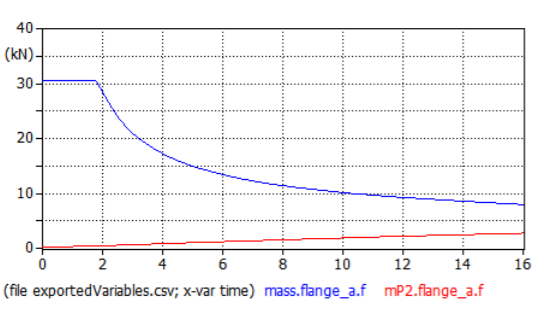
Come si vede nel tratto iniziale abbiamo la forza massima di trazione, che è pari a 30,5kN.
Colgo l’occasione per ricordare qui che la forza di scambio fra le ruote e l’asfalto non può essere illimitata: oltre un certo valore, come tutti sanno le ruote cominciano a slittare, e questo lo vogliamo assolutamente evitare. Si sa che la massima forza di scambio fra le ruote e l’asfalto, sia quando acceleriamo, che quando freniamo, non può superare un valore che è pari al peso dell’auto, moltiplicata per un coefficiente detto coefficiente di aderenza.
Qui ci sono delle questioni più complicate di quello che possiamo dire in questo articolo. Però possiamo stare tranquilli: nel caso della Tesla Plaid, in cui tutte le ruote sono motrici, quello che abbiamo detto sopra è sostanzialmente corretto. Il coefficiente di aderenza, per asfalti e ruote normali, in condizioni di asfalto in buone condizioni, asciutto e pulito è al più 1. Questo significa che la forza accelerante, per un’auto come la nostra che ha un
peso di 2322 kg, quindi circa 23 kN, la massima forza orizzontale può essere per l’appunto circa 23 kN, anche se il valore preciso dipende dalle caratteristiche e le condizioni di asfalto e pneumatici.
Comunque con particolari accorgimenti coefficienti di aderenza superiori ad 1 possono essere ottenuti. In Formula 1, con gomme e asfalti particolari si arriva a 1,5-1,6.
Come si risolve la questione? Il grafico qui sopra ci dice che la forza necessaria ad accelerare la Plaid per avere le massime prestazioni è molto superiore al peso stesso, in particolare del 34%!
E’ evidente che per ottenere quelle prestazioni le gomme e l’asfalto (o almeno uno dei due) devono essere speciali. Insomma, quasi come in formula 1. Questa considerazione è confermata dall’interessante articolo reperibile a questo link.
Quel che passa fra il modello e la realtà
In questo articolo abbiamo analizzato il funzionamento della Plaid sulla base di relazioni semplici e dati non ufficiali ottenuti da varie fonti. Con queste semplici formule e numeri abbiamo riprodotto abbastanza fedelmente i numeri disponibili sull’auto, ad es. il tempo per andare da 0 a 60 miglia per ora, o da 0 ad un quarto di miglio. Questo ci consente di essere fiduciosi che anche altri numeri che possiamo ottenere con questo modello, non noti precedentemente, siano abbastanza corretti.
Non bisogna illudersi che il modello che abbiamo fatto ci porti a precisione assoluta. La realtà è sempre estremamente complicata e i fenomeni che incidono su quello che si può misurare sperimentalmente sono tanti. E’ per questo che gli scienziati e gli ingegneri analizzano un modello su un certo sistema fisico o ingegneristico. Avere un modello significa avere delle formule matematiche che, sotto opportune ipotesi, descrivono abbastanza correttamente quello che si vuole analizzare.
Al crescere della precisione che si vuole ottenere occorre complicare e arricchire sempre di più il modello, per tener conto di fenomeni che incidono poco, ma che, a volere precisioni elevate, vanno considerate.
Solo per fare qualche esempio noi non abbiamo considerato:
– la dipendenza del coefficiente di attrito di rotolamento dalla velocità e dalla temperatura
– il cosiddetto scorrimento degli pneumatici sull’asfalto (quando siamo in trazione, soprattutto con un’auto come la Plaid, considerare un perfetto rotolamento è solo parzialmente accettabile
– il momento d’inerzia del motore e del riduttore (oltre che l’auto con la sua massa, anche le parti rotanti hanno un’inerzia)
– le perdite di energia che avvengono all’interno del riduttore.
Ma, ripeto, è sempre necessariamente così: si fa un modello di un fenomeno fisico nel quale si prendono in considerazione gli elementi più importanti, li si descrivono con delle equazioni matematiche, e si verifica che questo modello consenta di riprodurre abbastanza fedelmente i dati numerici di cui si dispone; a quel punto si usa il nostro modello per prevedere ulteriori dati non noti. Questo processo è indispensabile in
ingegneria, in quanto noi dobbiamo predire il comportamento di un certo sistema, ad es. un’auto, quando ancora non l’abbiamo realizzata; naturalmente quando poi l’avremo fatto, verificheremo sperimentalmente quanto abbiamo previsto.
O meglio verificheremo sperimentalmente di quanto quello che abbiamo realizzato si discosta da quello che abbiamo previsto. Perché pretendere una rispondenza assoluta sarebbe contemporaneamente stupido e inutile.
2-fine